20 热像仪的原理
20.1 简介
对大多数将要使用红外热像仪的用户而言,红外线辐射以及相关的热成像技术仍是一个新话题。在本节中,我们将与您一起探讨热像仪背后的原理。
20.2 电磁波谱
电磁波谱可任意划分成许多波长范围,这些波长范围称为波段,由产生和探测辐射的方法加以区分。电磁波谱的不同波段辐射之间没有本质区别。它们全部遵循相同的法则,唯一的区别仅在于波长不同。
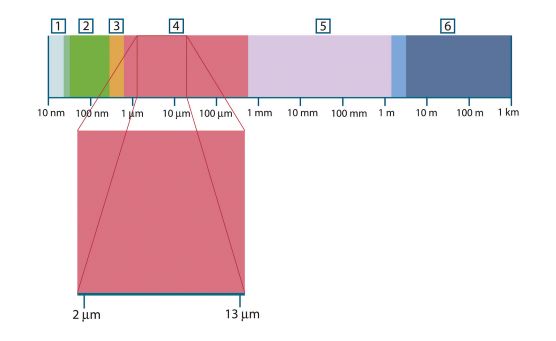
图 20.1 电磁波谱。1: X 射线;2:紫外线;3:可见光;4:红外线;5:微波;6:无线电波。
热像仪使用红外光谱波段。在短波长一端,其界限为深红色的视觉边界。在长波长一端,它与毫米范围内的微波无线电波长融为一体。
红外线波段通常可进一步划分为四个更小的波段,它们的界限也可任意选定。这四个波段是:近红外线波段 (0.75-3 μm)、中红外线波段 (3-6 μm)、远红外线波段 (6-15 μm) 和超远红外线波段 (15-100 μm)。虽然波长以 µm(微米)表示,但仍可使用其它计量单位来测量此光谱范围内的波长,如纳米 (nm) 和 Ångström (Å)。
不同波长测量单位之间的换算关系如下:
20.3 黑体辐射
黑体是一个可以吸收以任意波长照射在其上的所有辐射的物体。与发射辐射的物体有关的黑体一词由基尔霍夫定律(以 Gustav Robert Kirchhoff,1824-1887 的名字命名)阐明,它指出能够吸收任意波长的所有辐射的物体同样能够发射辐射。

图 20.2 Gustav Robert Kirchhoff (1824–1887)
黑体源的结构在原理上非常简单。由不透明吸收材料构成的等温线空腔孔隙的辐射特性几乎可以完全代表黑体的属性。完全辐射吸收体结构原理的实际应用包括一个一侧开有小孔的不透光暗箱。进入孔隙的任何辐射经多次反射被分散和吸收,只有极小一部分可能逸出。孔隙处获得的黑度几乎等于黑体,并且对于所有波长均近乎完全黑体。
通过提供此类等温线空腔及适当的热源,就构成了所谓的“空腔辐射体”。加热到相同温度的等温线空腔可以产生黑体辐射,其特性由空腔温度唯一确定。此类空腔辐射体通常用作实验室温度参照标准中的辐射源,用于标定诸如
FLIR Systems
热像仪之类的温度记录仪器。
如果黑体辐射的温度提高到 525°C 以上,则辐射源开始可见,因此在人眼看来将不再是黑色。这是辐射体的初始赤热温度,随着温度的进一步提高,辐射体随后会变为橙色或黄色。实际上,所谓的物体色温指的是黑体呈现相同外观时必须加热到的温度。
现在让我们研究一下描述黑体发射辐射的三个公式。
20.3.1 普朗克定律
图 20.3 Max Planck (1858–1947)
Max Planck (1858–1947) 使用下面的公式来描述黑体辐射的光谱分布:
此处:
|
Wλb
|
波长 λ 的黑体光谱辐射率。
|
|
c
|
光速 = 3 × 108 m/s
|
|
h
|
普朗克常数 = 6.6 × 10-34 焦耳秒。
|
|
k
|
玻尔兹曼常数 = 1.4 × 10-23 焦耳/K。
|
|
T
|
黑体的绝对温度 (K)。
|
|
λ
|
波长 (μm)。
|
根据普朗克公式绘制各种温度下的图形,可得到一系列的曲线。在任意一条普朗克曲线上,λ = 0 处的光谱辐射率为零,当波长为 λmax
时,光谱辐射率迅速增大到最大值,此后在长波长处又趋近于零。温度越高,则出现最大值的波长越短。
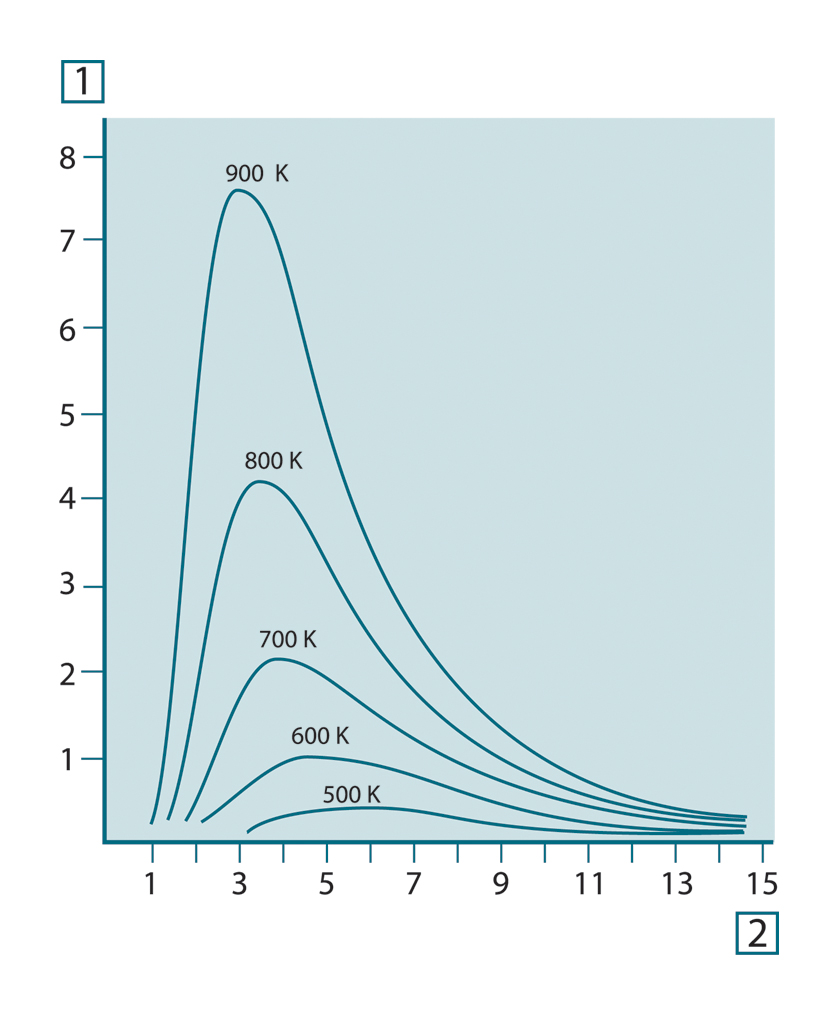
图 20.4 根据普朗克定律,在不同绝对温度下绘制的黑体光谱辐射率。1:光谱辐射率 (W/cm2 × 103(μm));2:波长 (μm)
20.3.2 维恩位移定律
针对 λ 对普朗克公式求微分并确定最大值,我们可以得出:
这就是维恩公式 (Wilhelm Wien, 1864-1928),它以算术形式表达随热辐射体温度的增大,颜色由红色到橙色或黄色变化的常见观测数据。颜色的波长与 λmax
计算所得的波长相同。通过应用近似计算 3 000/T μm,可得出指定黑体温度的一个有效近似 λmax
值。因此,炽热星体如天狼星 (11 000 K),发射出青白色的光线,在波长为 0.27 μm 的可见紫外光谱内其光谱辐射率达到峰值。

图 20.5 Wilhelm Wien (1864–1928)
太阳(约 6 000 K)发射黄色光,在可见光谱中央约 0.5 μm 处达到峰值。
在室温 (300 K) 下,辐射率在远红外线 9.7 μm 处达到峰值而在液态氮温度 (77 K) 下微量辐射率在超远红外波长 38 μm 处达到峰值。
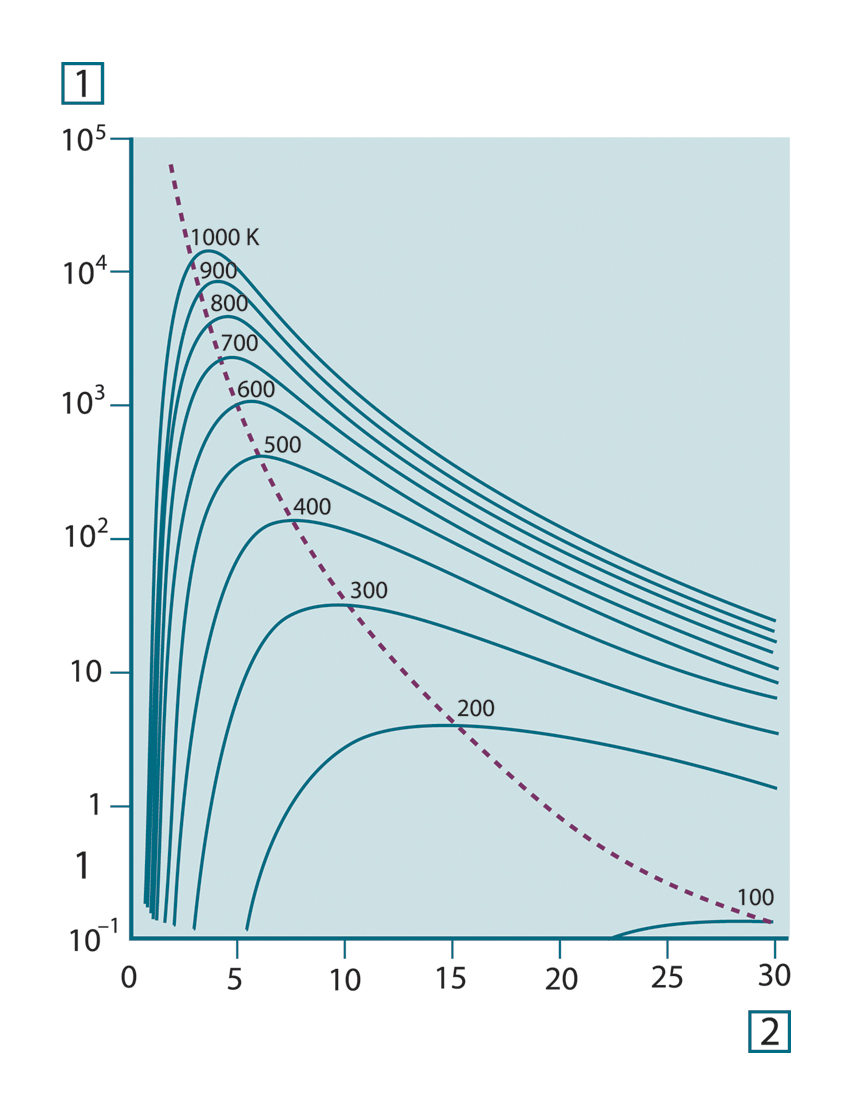
图 20.6 在 100 K - 1000 K 半对数范围下绘制的普朗克曲线。其中虚线表示由维恩位移定律描述的各种温度下的最大辐射率轨迹。1:光谱辐射率 (W/cm2 (μm));2:波长 (μm)。
20.3.3 史蒂芬-玻尔兹曼定律
通过从 λ = 0 到 λ = ∞ 对普朗克公式求积分,我们得出黑体的总辐射率 (Wb):
这就是史蒂芬-玻尔兹曼公式(以约瑟夫 史蒂芬 1835–1893 和路德维格 玻尔兹曼 1844–1906 的名字命名),它阐明黑体的总发射功率与其绝对温度的四次方成正比。Wb
在图形中表示特定温度下普朗克曲线下方的面积。可以看到,λ = 0 到 λmax
区间内的辐射率仅为总发射率的 25 %,表示位于可见光谱范围内大致的太阳辐射量。
图 20.7 Josef Stefan (1835–1893) 和 Ludwig Boltzmann (1844–1906)
通过使用史蒂芬-玻尔兹曼公式计算温度为 300 K 及外表面积约为 2 m2 下的人体辐射功率,得出值为 1 kW。此功率损失不是一成不变的,还需考虑在与体温相差不远的室温下的周围表面的辐射吸收,当然,还要考虑衣物的影响。
20.3.4 非黑体辐射源
迄今为止,我们仅讨论了黑体辐射源和黑体辐射。但是,真实物体在扩展波长范围内几乎从不遵守这些定律 – 虽然在某些波段内它们可能趋近于黑体行为。例如,某种白色涂料在可见光谱内完全显示为白色,但在波长约 2 μm 时则明显变成灰色,而在超过 3 μm 时更几乎显示为黑色。
真实物体会受三种作用的影响,使之表现与黑体不同的行为。其中,部分入射辐射 α 可能被吸收,部分 ρ 可能被反射,部分 τ 可能被透射。由于所有这些因素不同程度地取决于波长,我们使用下标 λ 来表示其定义中的光谱相关性。因此:
- 光谱吸收比 αλ = 物体吸收的光谱辐射功率与入射辐射功率的比率。
- 光谱反射比 ρλ = 物体反射的光谱辐射功率与入射辐射功率的比率。
- 光谱透射比 τλ = 从物体透射的光谱辐射功率与入射辐射功率的比率。
对于任意波长,这三个系数之和必须始终等于 1,因此我们得出下面的关系式:
对于不透明材料, τλ
= 0,所以此关系式可简化为:
描述物体在特定温度下产生的黑体辐射率的部分 ε,还需使用另一个名为辐射比的系数。因此,我们引入下面的定义:
光谱辐射比 ελ
= 物体发射的光谱辐射功率相对同温和同波长下的的黑体辐射功率的比率。
用算术方法表示,此定义可表述为物体光谱辐射率与黑体辐射率之比,如下所示:
一般而言,辐射源存在三种类型,它们由随波长变化的光谱辐射方式加以区分。
- 黑体,其 ελ = ε = 1
- 灰体,其 ελ = ε = 小于 1 的常数
- 选择性辐射体,其 ε 随波长变化。
根据基尔霍夫定律,任意材料在任意指定温度和波长下的物体光谱辐射比和光谱吸收比相等。即:
从此公式推断,不透明材料的计算公式如下(因为 αλ + ρλ = 1):
由于高度抛光材料的 ελ
趋近于零,因此完全反射材料(即完全镜面)的计算公式如下:
对于灰体辐射源,史蒂芬-玻尔兹曼公式演变成:
这表明灰体的总辐射功率等于同温下黑体的辐射功率乘于灰体的 ε 值。
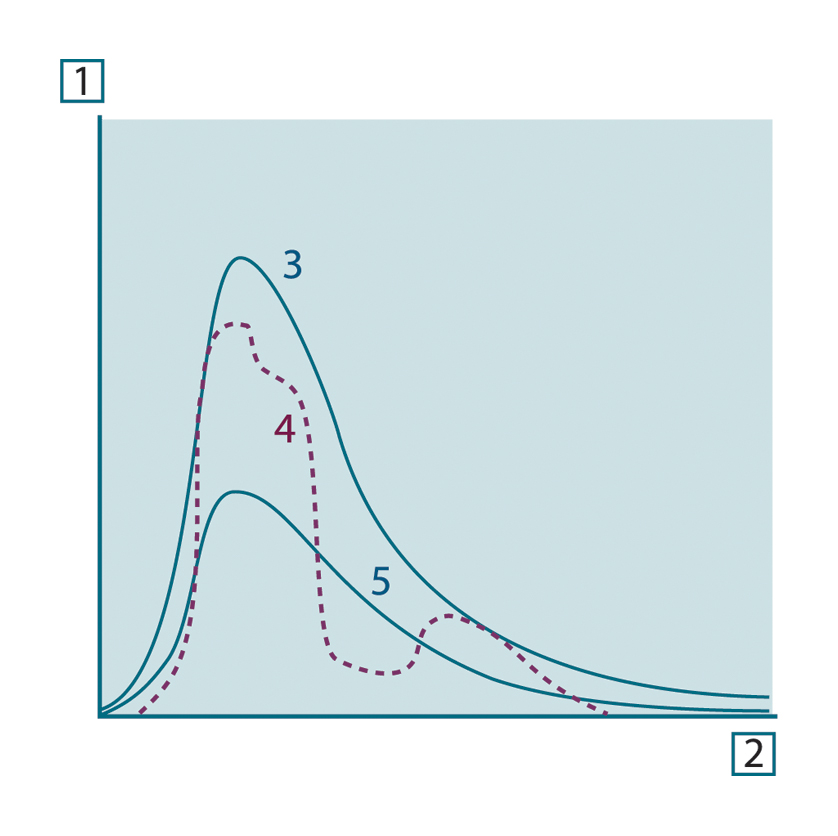
图 20.8 三种辐射源类型的光谱辐射率。1:光谱辐射率;2:波长;3:黑体;4:选择性辐射体;5:灰体。
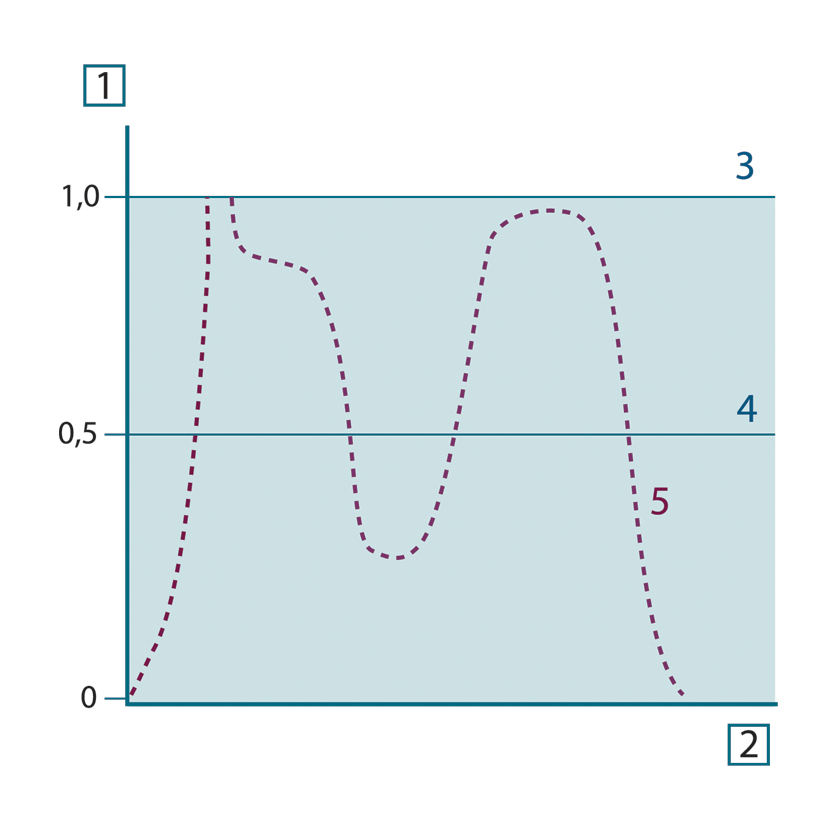
图 20.9 三种辐射源类型的光谱辐射比。1:光谱辐射比;2:波长;3:黑体;4:灰体;5:选择性辐射体。
20.4 红外线半透明材料
现在我们研究一下半透明非金属物体,如厚塑料平板。当该平板加热时,其体内产生的辐射必须经材料通向表面,在此过程中部分辐射将被吸收。当到达表面时,部分辐射还会反射回内部。反射回的部分辐射再次被吸收,但其中的一部分会到达其它表面并逸出,而部分辐射再次被反射。虽然此渐进反射过程逐渐变弱,但在计算平板的总辐射率时,所有过程均必须计算在内。将所得几何级数相加,我们得到半透明平板的有效辐射率:
如果平板为不透明材料,则此公式可简化成下面的简单公式:
此最终关系式使用起来非常简便,因为相比直接测量辐射比,测量反射比通常要容易得多。