31 Termografiteori

31.1 Inledning

Ämnesområdet infraröd strålning och den termografiteknik som används inom området är fortfarande nytt för många som kommer att använda en värmekamera. I det här avsnittet beskrivs teorin bakom termografi.

31.2 Det elektromagnetiska spektrat

Det elektromagnetiska spektrat delas godtyckligt in i ett antal våglängdsområden som kallas band och som särskiljs via de metoder som används för att skapa och upptäcka strålning. Det finns ingen grundläggande skillnad mellan strålning i olika band i det elektromagnetiska spektrat. De styrs alla av samma lagar och det enda som skiljer är våglängden.

Figur 31.1 Det elektromagnetiska spektrat. 1: Röntgen; 2: UV; 3: Synlig; 4: IR; 5: Mikrovågor; 6: Radiovågor.

Termografi arbetar med det infraröda våglängdsområdet. Dess nedre del tangerar visuella våglängder (mörkrött ljus)‎ medan dess övre del närmar sig mikrovågor med våglängder omkring en millimeter.

Det infraröda bandet delas ofta upp i fyra mindre band,‎ vilkas gränser också väljs godtyckligt. De innefattar: det nästan infraröda (0,‎75–3 μm)‎,‎ det medelinfraröda (3–6 μm)‎,‎ det mycket infraröda (6–15 μm)‎ och det extremt infraröda (15–100 μm)‎. Även om våglängderna anges i μm (mikrometer)‎ används ofta andra enheter för att mäta våglängder i det här spektralområdet,‎ t.ex. nanometer (nm)‎ och Ångström (Å)‎.

Förhållandet mellan de olika enheterna är:

31.3 Svartkroppsstrålning

En svartkropp definieras som ett objekt som absorberar all inkommande strålning oavsett våglängd. Den missvisande benämningen svart syftar på ett objekt som avger strålning och förklaras av Kirchhoffs lag (efter Gustav Robert Kirchhoff,‎ 1824–1887)‎,‎ som konstaterar att en kropp som är kapabel att absorbera all strålning i samtliga våglängdsområden även är lika kapabel att avge strålning.

Figur 31.2 Gustav Robert Kirchhoff (1824–1887)‎

En svartkroppskällas konstruktion är i princip väldigt enkel. Strålningsegenskaperna hos en öppning i en termiskt jämn kavitet gjord av ett ogenomskinligt absorberande material är nästan samma som egenskaperna hos en svartkropp. En praktisk tillämpning av principen av konstruktion för ett objekt med total absorbering av strålning består av en låda som är helt försluten på alla sidor men med en minimal öppning på en av sidorna. Den strålning som kommer in genom öppningen skingras och absorberas av upprepade reflektioner,‎ vilket gör att endast en oändligt liten del kan försvinna. Svärtan vid öppningen är nästan identisk med den hos en svartkropp och nästan perfekt för alla våglängdsområden.

Genom att förse en sådan termiskt jämn kavitet med en passande värmekälla blir det en kavitetsstrålare. En termiskt jämn kavitet uppvärmd till en enhetlig temperatur genererar svartkroppsstrålning vars egenskaper endast bestäms av kavitetstemperaturen. Sådana kavitetsstrålare används ofta som källor till strålning för temperaturreferensstandard i laboratoriet för att kalibrera termografiska instrument,‎ t.ex. en kamera från FLIR Systems.

Om temperaturen hos en svartkroppsstrålare stiger till mer än 525 °C närmar sig källan det synliga området och ögat uppfattar den därför inte som svart. Det är strålarens begynnande rödglödstemperatur som sedan blir orange eller gul allteftersom temperaturen stiger. Begreppet färgtemperatur refererar till hur mycket en svartkroppsstrålare måste värmas upp för att anta en viss färg.

Beakta följande tre formler som beskriver strålningen från en svartkropp.

31.3.1 Plancks lag

Figur 31.3 Max Planck (1858–1947)‎

Max Planck (1858–1947)‎ beskrev de spektrala proportionerna hos strålningen från en svartkropp med följande formel:

där:

Wλb	Svartkroppens spektrala emittans vid våglängden λ.
c	Ljusets hastighet = 3 × 108 m/s.
h	Plancks konstant = 6,‎6 × 10-34 Js.
k	Boltzmanns konstant = 1,‎4 × 10-23 J/K.
T	Svartkroppens absoluta temperatur i Kelvingrader (K)‎.
λ	Våglängd (μm)‎.

Om man grafiskt åskådliggör resultaten från Plancks formel vid ett antal olika temperaturer får man en serie kurvor. Följer man vilken kurva som helst ser man att den spektrala strålningen är noll då λ = 0 varefter den ökar snabbt för att nå ett maximum vid våglängden λmax och åter närmar sig noll vid mycket långa våglängder. Ju högre temperatur,‎ desto kortare är den våglängd där maximum nås.

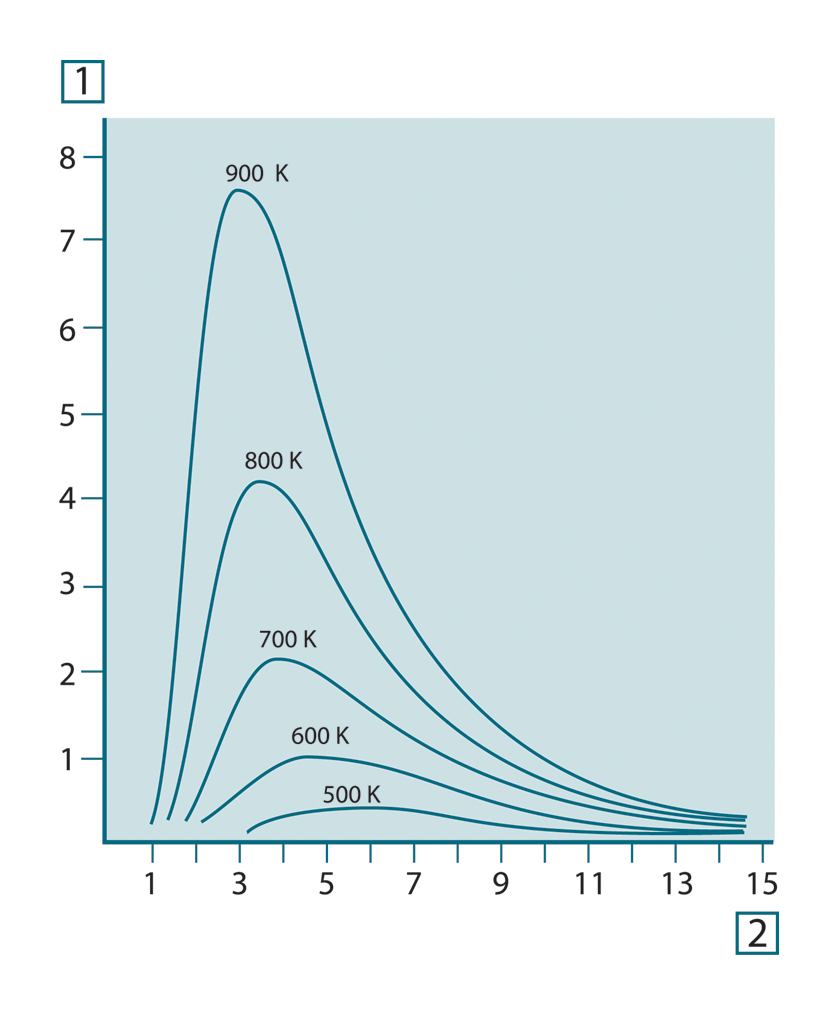
Figur 31.4 En svartkropps spektrala strålning,‎ enligt Plancks lag,‎ grafiskt åskådliggjord vid olika temperaturer. 1: Spektral emittans (W/cm2 × 103(μm)‎)‎; 2: Våglängd (μm)‎

31.3.2 Wiens förskjutningslag

Genom att derivera Plancks lag med avseende på λ och finna maximum får vi följande:

Det här är Wiens förskjutningslag (efter Wilhelm Wien,‎ 1864–1928)‎ som matematiskt uttrycker det faktum att färgen varierar från röd till orange eller gul när temperaturen på en termisk strålare stiger. Färgens våglängd är samma som våglängden som beräknats för λmax. Ett bra ungefärligt värde på λmax vid en given svartkroppstemperatur fås genom att tillämpa tumregeln 3 000/T μm. En väldigt het stjärna som Sirius (11 000 K)‎,‎ som avger ett blåvitt ljus,‎ strålar därför med ett maximum av spektral emittans som uppstår inom det osynliga,‎ ultravioletta området vid våglängden 0,‎27 μm.

Figur 31.5 Wilhelm Wien (1864–1928)‎

Solen (ca 6 000 K)‎ avger gult ljus och når sitt maximum vid ungefär 0,‎5 μm i mitten av det synliga ljusspektrat.

Vid rumstemperatur (300 K)‎ ligger maximum för strålningen vid 9,‎7 μm i det mycket infraröda,‎ medan maximum inträffar vid 38 μm i de extremt infraröda våglängderna vid temperaturen för flytande kväve (77 K)‎.

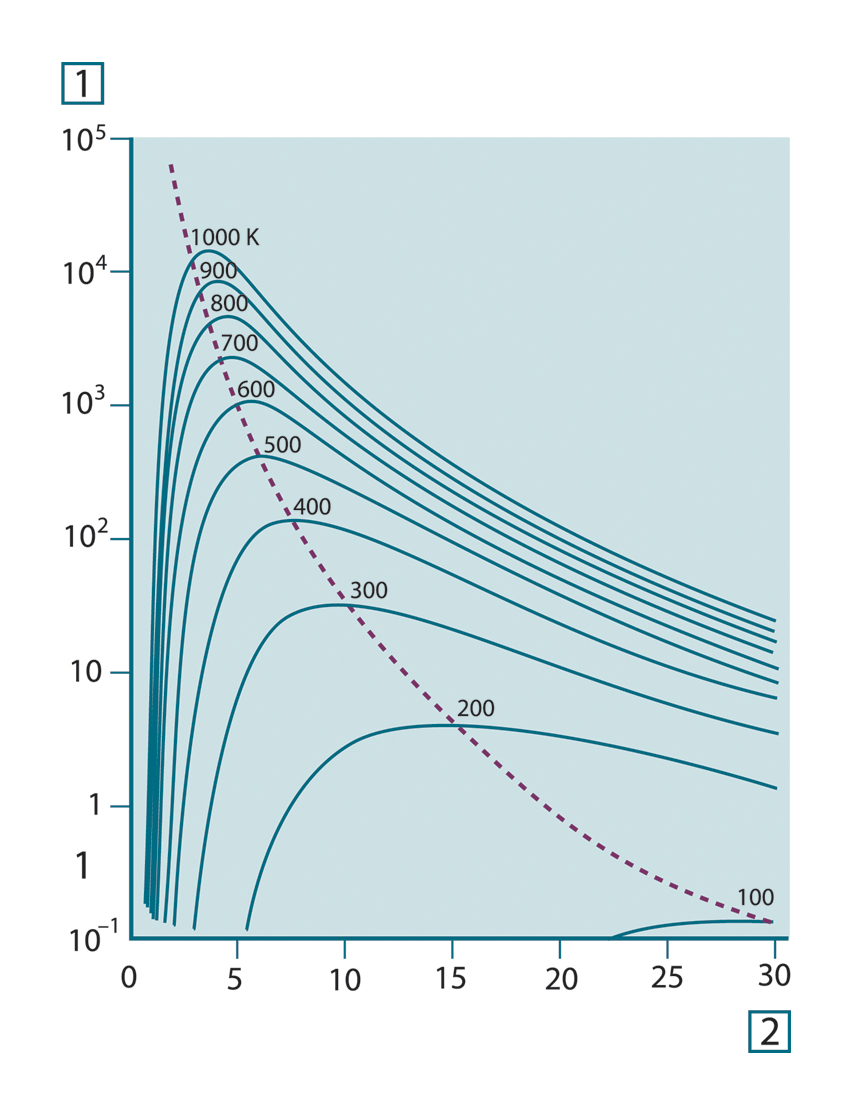
Figur 31.6 Plancks kurvor grafiskt åskådliggjorda längs en semilogaritmisk skala mellan 100 K och 1 000 K. De prickade kurvorna markerar punkten för den maximala strålningen vid varje temperatur,‎ enligt Wiens förskjutningslag. 1: Spektral emittans (W/cm2 (μm)‎)‎; 2: Våglängd (μm)‎.

31.3.3 Stefan-Boltzmanns lag

Genom att integrera Plancks formel från λ = 0 till λ = ∞ får vi den totala strålningen (Wb)‎ hos en svartkropp:

Detta är Stefan-Boltzmanns formel (efter Josef Stefan,‎ 1835–1893,‎ och Ludwig Boltzmann,‎ 1844–1906)‎,‎ som säger att den totala emissiviteten hos en svartkropp är proportionell i förhållande till den fjärde kraften av dess absoluta temperatur. Grafiskt motsvarar Wb rområdet nedanför Planck-kurvan vid en given temperatur. Det kan visas att emittansen i intervallet λ = 0 to λmax endast är 25 % av den totala strålningen,‎ vilket ungefär motsvarar solens strålning inom det synliga våglängdsområdet.

Figur 31.7 Josef Stefan (1835–1893)‎ och Ludwig Boltzmann (1844–1906)‎

Genom att använda Stefan-Boltzmanns formel för att beräkna den effekt som en människas kropp avger vid en temperatur av 300 K och en total yta på ca 2 m2 får vi 1 kW. Denna värmeförlust skulle kroppen inte kunna klara av om den inte kompenserade förlusten genom absorption av strålning från omgivningen som normalt har nästan samma temperatur,‎ samt genom det skydd som klädernas isolering erbjuder.

31.3.4 Icke-svartkroppsstrålare

Hittills har endast svartkroppsstrålare och svartkroppsstrålning beskrivits. Verkliga objekt följer emellertid sällan de här lagarna över ett längre våglängdsområde – även om de närmar sig svartkroppens egenskaper i vissa spektrala områden. Ett exempel är att en viss typ av vit färg kan se helt vitut i det synliga våglängdsområdet medan den blir helt gråvid ca 2 μm och bortom 3 μm är nästan svart.

Det finns tre omständigheter som kan förhindra att ett verkligt objekt uppför sig som en svartkropp: en bråkdel av den infallande strålningen α kan absorberas,‎ en bråkdel ρ kan reflekteras och en bråkdel τ kan överföras. Eftersom alla dessa faktorer är mer eller mindre våglängdsberoende används tecknet λ för att markera detta beroende. Följaktligen:

Den spektrala absorptionen αλ= kvoten mellan den spektrala strålningen som ett objekt absorberar och den totala strålning det utsätts för.
Den spektrala reflektionen ρλ= kvoten mellan den spektrala strålningen som ett objekt reflekterar och den totala strålning det utsätts för.
Den spektrala transmissionen τλ= kvoten mellan den spektrala strålning som överförs via ett objekt och den totala strålning det utsätts för.

Summan av dessa tre faktorer måste alltid bli 1 vid alla våglängder vilket ger oss följande formel:

För ogenomskinliga material är τλ = 0 och formeln kan förenklas till:

En annan faktor,‎ emissiviteten,‎ krävs för att beskriva bråkdelen ε av den spektrala strålning som ett objekt producerar vid en viss temperatur,‎ jämfört med strålningen från en svartkropp vid samma temperatur. Sålunda får vi följande definition:

Den spektrala emissiviteten ελ = kvoten mellan den spektrala strålningen från ett objekt och den från en svartkropp med samma temperatur och våglängd.

Uttryckt matematiskt kan det skrivas som kvoten mellan objektets och svartkroppens spektrala strålning på följande sätt:

Generellt sett kan man säga att de finns tre typer av strålningskällor som skiljs åt av de olika våglängderna vid spektral emittans.

En svartkropp för vilken ελ = ε = 1
En gråkropp för vilken ελ = ε = en konstant mindre än 1
En selektiv strålare för vilken ε varierar med våglängden

Enligt Kirchhoffs lag är spektral emissitivet och spektral absorption för en kropp lika vid alla temperaturer och våglängder,‎ det vill säga:

Då får vi,‎ för ett ogenomskinligt material (eftersom αλ +‎ ρλ = 1)‎:

För högglanspolerade material närmar sig ελ noll,‎ vilket för perfekt reflekterande material (dvs. en spegel)‎ skulle ge:

För gråkroppsstrålare blir Stefan-Boltzmanns formel:

Det betyder att den totala emissiviteten för en gråkropp är samma som för en svartkropp vid samma temperatur minskad proportionellt till värdet på ε hos gråkroppen.

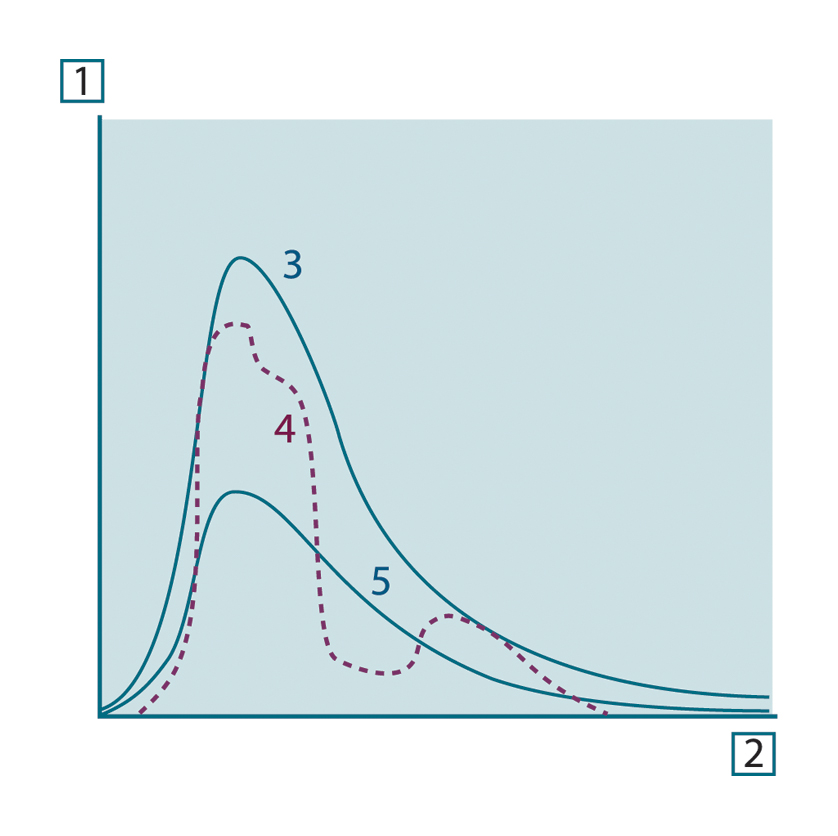
Figur 31.8 Spektral emittans för tre typer av strålare. 1: Spektral emittans; 2: Våglängd; 3: Svartkropp; 4: Selektiv strålare; 5: Gråkropp.

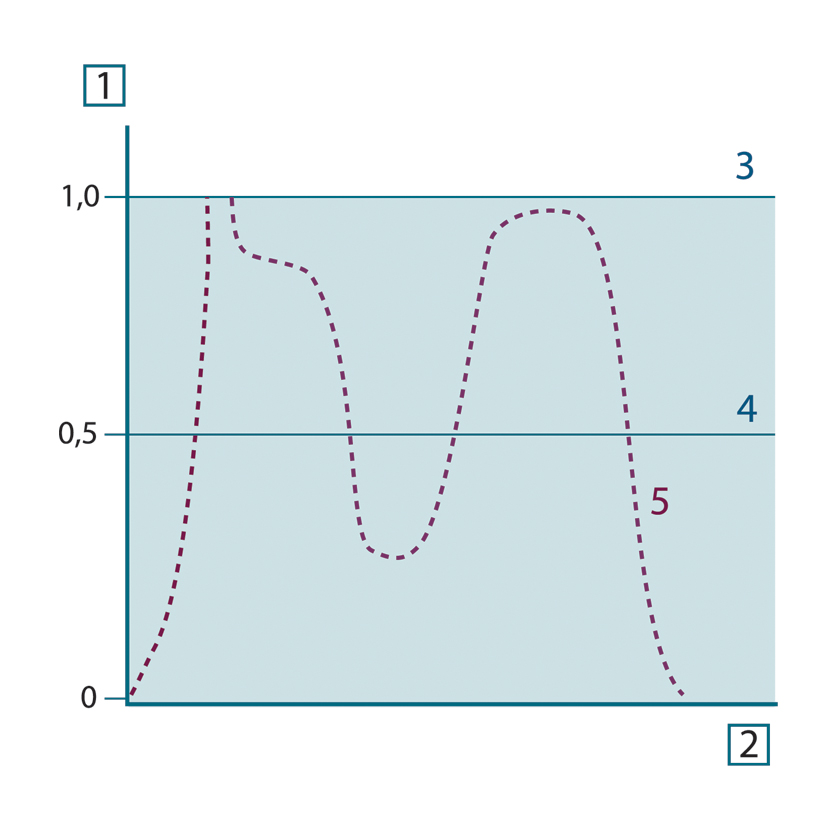
Figur 31.9 Spektral emissivitet för tre typer av strålare. 1: Spektral emissivitet; 2: Våglängd; 3: Svartkropp; 4: Gråkropp; 5: Selektiv strålare.

31.4 Infraröda halvtransparenta material

Tänk på en icke-metallisk,‎ halvtransparent kropp – t.ex. en tjock,‎ plan plastplatta. När plattan värms upp måste den strålning som uppstår i plattans inre ta sig igenom materialet mot ytan,‎ där den delvis absorberas. När strålningen når ytan återreflekteras en del av den till plattans inre. Den återreflekterade strålningen absorberas delvis men en del av den når till den andra ytan där det mesta av den försvinner; en del av den återreflekteras igen. Även om reflektionerna blir svagare och svagare måste de räknas in om man ska beräkna den totala strålningen hos plattan. När den geometriska serien summeras fås den effektiva emissiviteten hos en halvtransparent platta på följande sätt:

När plattan blir ogenomskinlig reduceras formeln till följande enkla formel:

Den sista formeln är praktisk eftersom det ofta är enklare att mäta reflektion än emissivitet direkt.