32 Mätformeln
Som vi redan nämnt tar kameran när den är inriktad mot ett objekt inte bara emot strålning från objektet. Den fångar också
upp den strålning från omgivningen som reflekteras mot objektets yta. Båda de här strålningsbidragen dämpas i viss utsträckning
av atmosfären på mätvägen. Till detta kommer ett tredje strålningsbidrag från själva atmosfären.
Den här beskrivningen av mätsituationen, ger en ganska rättvisande bild av de verkliga förhållandena (se vidare figuren nedan).
Vissa faktorer är dock inte medtagna, t.ex. solljusets spridning i atmosfären eller vagabonderande strålning från starka
strålningskällor utanför synfältet. Störningar av de här slagen är svåra att kvantifiera, men lyckligtvis är de normalt så
små att de kan försummas. Om de inte är försumbara är mätkonfigurationen sannolikt sådan att risken för störningar är uppenbar,
åtminstone för en erfaren operatör. Han måste då på eget initiativ förändra mätsituationen så att störningarna elimineras,
t.ex. genom att ändra kamerariktningen, skärma av starka strålningskällor osv.
Om vi godtar den här beskrivningen kan vi med hjälp av figuren nedan härleda en formel för att beräkna objektets temperatur
med ledning av den kalibrerade utsignalen från kameran.
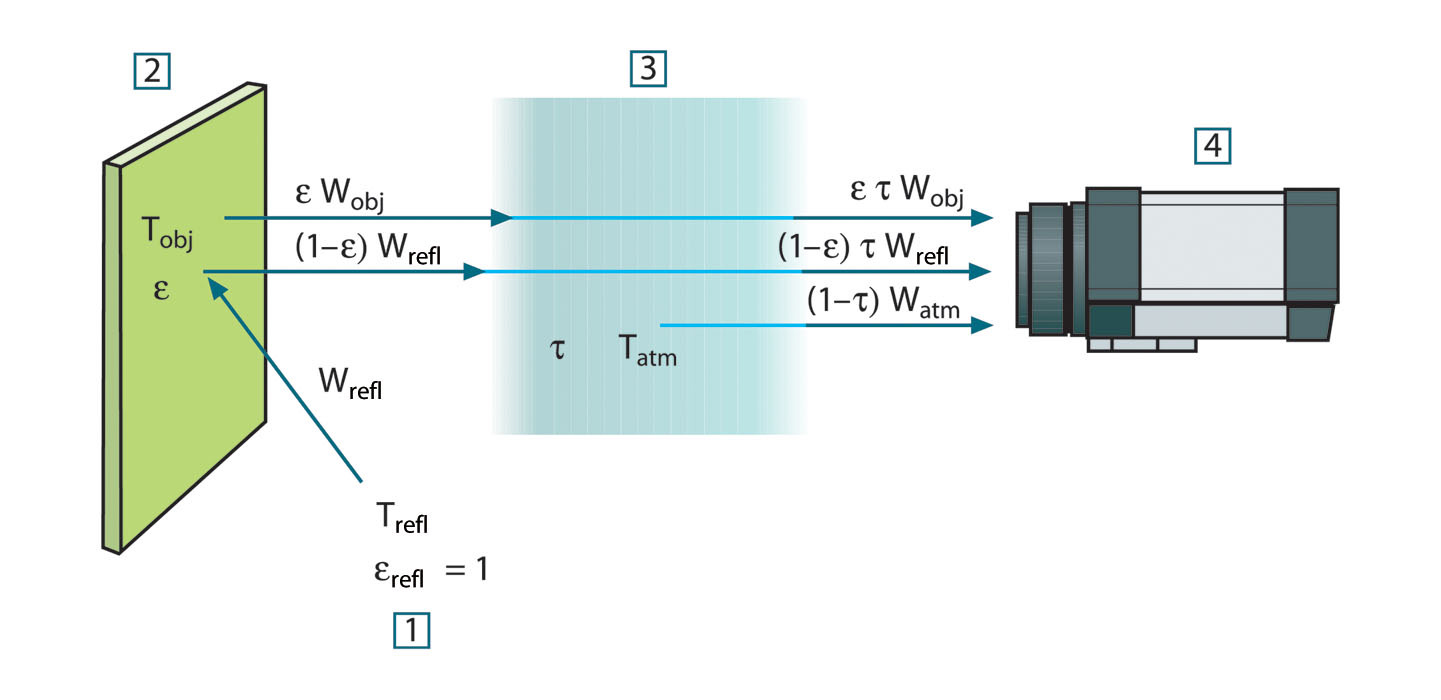
Figur 32.1 En schematisk framställning av den allmänna termografiska mätsituationen.1: Omgivning; 2: Objekt; 3: Atmosfär; 4: Kamera
Anta att den mottagna strålningseffekten W från en svartkroppstemperaturkälla Tsource på kort avstånd genererar en utsignal från kameran Usource som är proportionell mot den inkommande effekten (effektlinjär kamera). Vi kan då skriva (ekvation 1):
Eller, förenklat:
där C är en konstant.
Om källan istället är en gråkropp med emittansen ε blir den mottagna strålningen följaktligen lika med εWsource.
Vi kan nu skriva de tre termerna för mottagen strålningseffekt:
- Emission från objektet = ετWobj, där ε är objektets emittans och τ är atmosfärens transmittans. Objektets temperatur är Tobj.
- Reflekterad emission från omgivningskällor = (1 – ε)τWrefl, där (1 – ε) är objektets reflektans. Omgivningskällorna har temperaturen Trefl. Vi har här antagit att temperaturen Trefl är densamma för alla emitterande ytor inom en halvsfär med medelpunkten på objektets yta. Detta kan naturligtvis innebära en förenkling av den verkliga situationen. Förenklingen är dock nödvändig för att vi ska kunna härleda en hanterbar formel, och Trefl kan – åtminstone teoretiskt – ges ett värde som motsvarar den effektiva temperaturen hos en komplex omgivning.Lägg också märke till att vi har antagit emittansen = 1 för omgivningen. Detta är korrekt enligt Kirchhoffs lag: All strålning som faller in mot de omgivande ytorna kommer med tiden att absorberas av samma ytor. Emittansen är alltså = 1 (observera dock att det sistnämnda resonemanget kräver att hela sfären kring objektet beaktas).
- Emission från atmosfären = (1 – τ)τWatm, där (1 – τ) är atmosfärens emittans. Atmosfärens temperatur är Tatm.
Den totala mottagna strålningseffekten kan nu skrivas (ekvation 2):
Multiplicera varje term med konstanten C i ekvation 1 och ersätt CW-produkterna med motsvarande U enligt samma ekvation. Vi får (ekvation 3):
Lös ut Uobj ur ekvation 3 (ekvation 4):
Detta är den allmänna mätformel som används i all termografisk utrustning från FLIR Systems. Spänningarna i formeln är:
Tabell 32.1 Spänningar
|
Uobj
|
Beräknad kamerautspänning för en svartkropp med temperaturen Tobj, dvs. en spänning som direkt kan omvandlas till en verklig sökt objekttemperatur.
|
|
Utot
|
Uppmätt kamerautspänning i det aktuella fallet.
|
|
Urefl
|
Teoretisk kamerautspänning för en svartkropp med temperaturen Trefl enligt kalibreringen.
|
|
Uatm
|
Teoretisk kamerautspänning för en svartkropp med temperaturen Tatm enligt kalibreringen.
|
Operatören måste mata in ett antal parametervärden för beräkningen:
- objektets emittans ε
- den relativa luftfuktigheten
- Tatm
- objektavståndet (Dobj)
- den (effektiva) temperaturen hos objektets omgivning eller den reflekterade omgivningstemperaturen Trefl, samt
- atmosfärens temperatur Tatm
Detta kan innebära mycket arbete för operatören, eftersom det vanligen inte finns några enkla sätt att bestämma noggranna
värden för emittans och atmosfärtransmittans i det enskilda fallet. De två temperaturerna är normalt mindre problematiska,
förutsatt att det inte finns några stora och intensiva strålningskällor i omgivningen.
En naturlig fråga i detta sammanhang är: Hur viktigt är det att känna till de rätta värdena på parametrarna? Det kan vara
intressant att redan här få en uppfattning om problemet genom att titta på några olika mätfall och jämföra de relativa magnituderna
hos de tre strålningstermerna. Det kan ge oss en indikation på när det är viktigt att använda korrekta värden på olika parametrar.
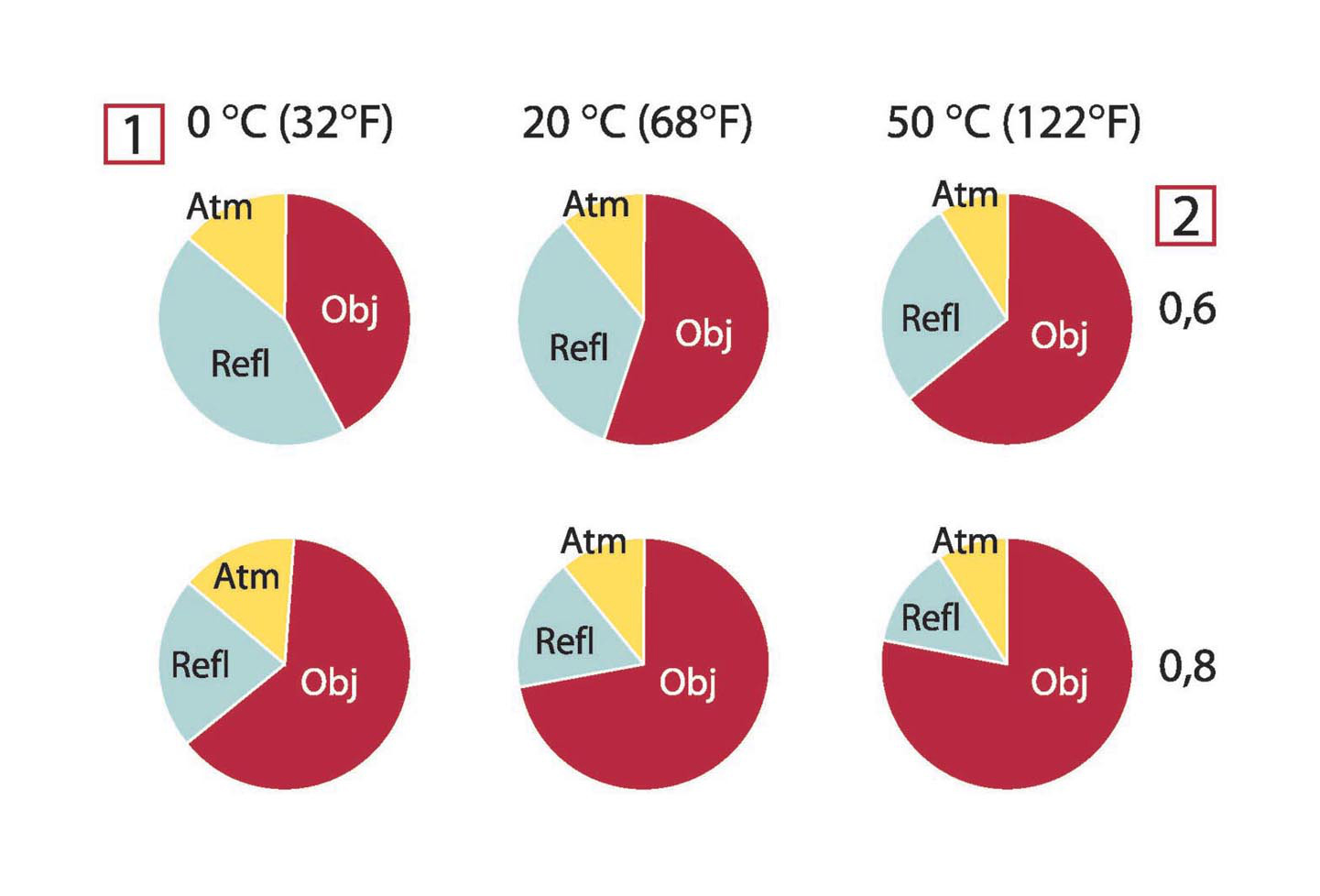
Figurerna nedan visar de relativa magnituderna hos de tre strålningsbidragen för tre olika objekttemperaturer, två emittanser
och två spektrumområden: KV och LV. De återstående parametrarna har följande fasta värden:
- τ = 0,88
- Trefl = +20 °C
- Tatm = +20 °C
Det är uppenbart att en korrekt temperaturmätning är mer avgörande vid låga objekttemperaturer än vid höga, eftersom ”störningsstrålningskällorna”
relativt sett är mycket starkare i det förstnämnda fallet. Om dessutom objektets emittans är låg blir situationen ännu besvärligare.
Till sist måste vi besvara frågan om betydelsen av att få använda kalibreringskurvan ovanför den högsta kalibreringspunkten,
alltså vad vi kallar att extrapolera. Anta att vi i ett visst fall mäter Utot = 4,5 volt. Kamerans högsta kalibreringspunkt låg vid ungefär 4,1 volt, vilket operatören inte kände till. Även om objektet
hade varit en svartkropp, dvs. Uobj = Utot, gör vi alltså i själva verket en extrapolering av kalibreringskurvan när vi omvandlar 4,5 volt till en temperatur.
Anta nu att objektet inte är svart utan har emittansen 0,75, och att transmittansen är 0,92. Vi antar också att de två
andra termerna i ekvation 4 tillsammans blir 0,5 volt. Om vi beräknar Uobj med ekvation 4 får vi då Uobj = 4,5 / 0,75 / 0,92 – 0,5 = 6,0. Det är en ganska extrem extrapolering, särskilt med tanke på att videoförstärkaren
kanske begränsar utspänningen till 5 volt! Observera dock att tillämpningen av kalibreringskurvan är en teoretisk procedur
som kan användas när det inte finns några elektroniska eller andra begränsningar. Vi litar på att kameran, om den inte hade
haft några signalbegränsningar, och om den hade kalibrerats för långt högre spänningar än 5 volt, hade haft en kalibreringskurva
som i stort sett hade sett likadan ut som vår verkliga kurva när vi extrapolerade den ovanför 4,1 volt, förutsatt att kalibreringsalgoritmen
i likhet med FLIR Systems algoritm är baserad på strålningsfysikalgorithm. Givetvis måste man sätta en gräns för sådana extrapoleringar.
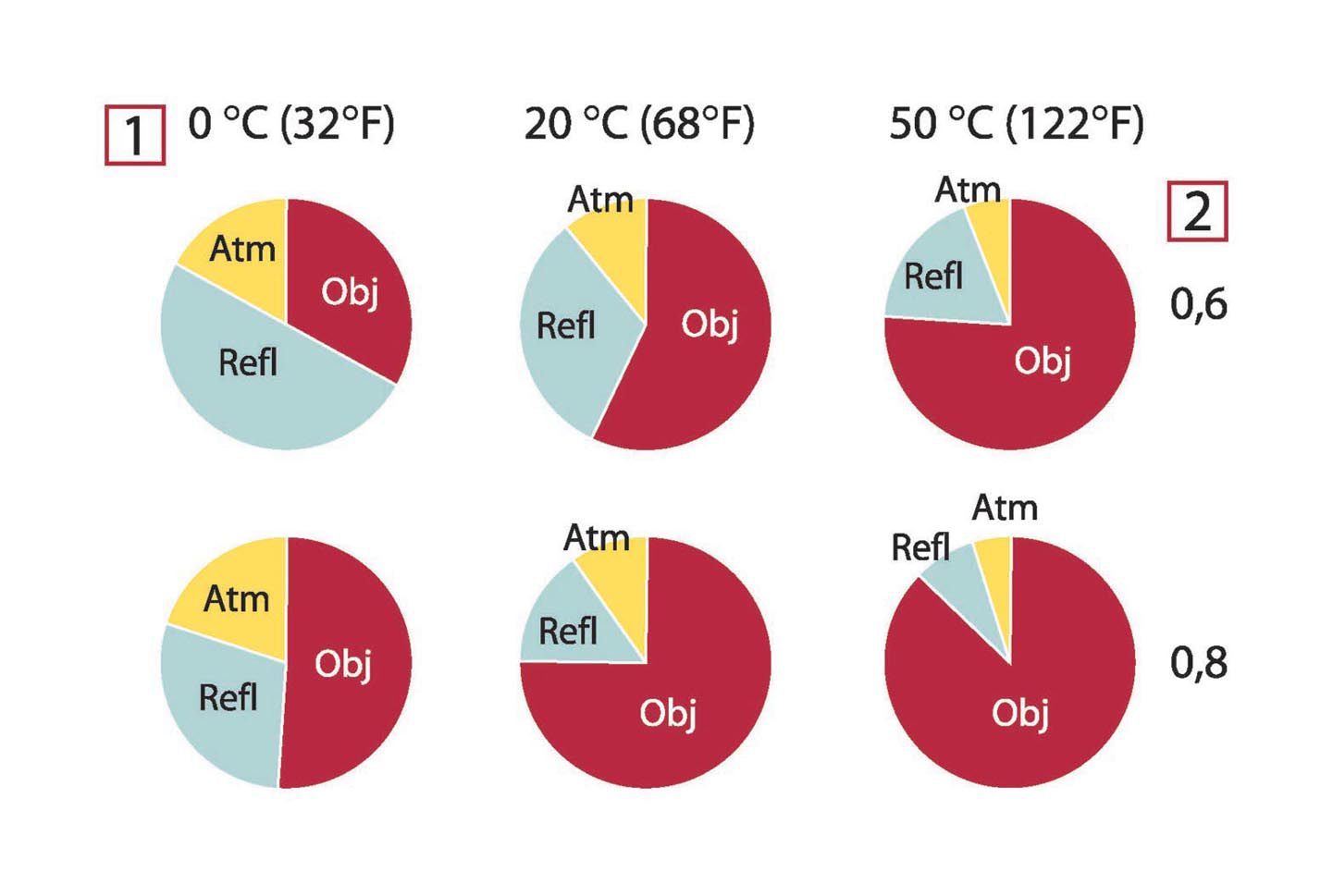
Figur 32.2 Relativa magnituder hos strålningskällor under varierande mätförhållanden (KV-kamera). 1: Objektets temperatur; 2: Emittans; Obj: Objektets strålning; Refl: Reflekterad strålning; Atm: atmosfärstrålning. Fasta parametrar: τ = 0,88; Trefl = 20 °C; Tatm = 20 °C.